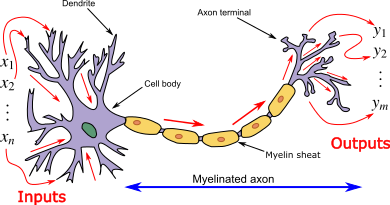
Apprentissage machine

John Samuel
CPE Lyon

Year: 2022-2023
Email: john(dot)samuel(at)cpe(dot)fr

Intelligence Artificielle [Pan 2016, Jaakkola 2019]

• La méthode d'apprentissage profond
• les fusions et acquisitions d'entreprises
  • DNNresearch par Google
  • LinkedIn par Microsoft
• Les chatbots
  • Xiaobing par Microsoft
• Les programmes de jeux
  • AlphaGo par Google
• L'utilisation dans les hôpitaux
  • Watson par IBM
• La compréhension du langage naturel
  • Baidu

Intelligence Artificielle [Pan 2016, Jaakkola 2019]

• 1956: la definition d'IA
  • Proposée par J. McCarthy, M. L. Minsky, H. Simon, A. Newell, C. E. Shannon, N. Rochester,...
  • La capacité des machines à comprendre, à penser et à apprendre d'une manière similaire à celle des êtres humains,
• 1970-2000
  • 1983: le rapport par James Lighthill
  • 1982-1992: l'échec du développement d'un ordinateur intelligent par le Japon
  • 1984: la construction manuelle d'une encyclopédie de la connaissance (Cyc) par Stanford

Intelligence Artificielle 2.0 [Pan 2016, Jaakkola 2019]

• 1990s-présent
  • Popularité de l'Internet
  • l'utilisation des capteurs
  • Big Data
  • l'e-commerce
• Des demandes sociales pour IA
  • des villes intelligentes
  • médecine
  • transport
  • les automobiles sans conducteur
  • les smartphones

Intelligence Artificielle 2.0 [Pan 2016]

• les technologies à l'origine de l'IA
  • L'IA basée sur des données massives (Big Data)
  • L'intelligence de la foule sur Internet
  • Le savoir médiatique croisé
  • L'intelligence hybride homme-machine
  • Systèmes autonomes et intelligents
• L'avenir
  • L'IA explicative et générique
  • la cognition, l'apprentissage et l'inférence trans-médiatiques.
  • l'intelligence communautaire à partir de l'intelligence des foules basée sur l'intelligence individuelle
  • des systèmes autonomes et intelligents pour le développement de machines et de produits intelligents.

Objectifs

Objectifs

1. Apprentissage machine
2. Apprentissage profond
3. Intelligence artificielle

3 approches

1. Apprentissage supervisé: disponibilité des données de formation labellisées
2. Apprentissage non supervisé: aucune donnée de formation labellisée n'est disponible
3. Apprentissage semi-supervisé: un petit ensemble de données de formation étiquetées et une grande quantité de données non étiquetées

Formalisation

• Vecteur euclidien: objet géométrique avec magnitude et direction
• Espace vectoriel: collection de vecteurs qui peuvent être additionnés et multipliés par des nombres
• Vecteur de caractéristiques (features): vecteur n-dimensionnel
• Espace de caractéristiques: Espace vectoriel associé aux vecteurs

Exemples de caractéristiques

• Images: les valeurs des pixels.
• Textes: Fréquence d'apparition des phrases textuelles.

Formalisation

• Construction de caractéristiques¹: construction de nouvelles fonctionnalités à partir de caractéristiques déjà disponibles
• Opérateurs de construction pour les caractéristiques
  • Opérateurs d'égalité, opérateurs arithmétiques, opérateurs de tableau (min, max, moyenne, etc.)...

Example

• Soit Année de naissance et Année de décès deux caractéristiques existantes.
• Une nouvelle caractéristique appelée âge est créée. âge = Année de décès - Année de naissance

1. https://en.wikipedia.org/wiki/Feature_vector

Formalisation: Apprentissage supervisé

• Soit \(N\) le nombre d'exemples d'entraînement
• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• Soit \({(x_1, y_1),...,(x_N, y_N)}\) les \(N\) exemples d'entraînement, où
  • \(x_i\) est le vecteur de caractéristiques de i^ème exemple d'entraînement.
  • \(y_i\) est son label.
• L'objectif de l'algorithme d'apprentissage supervisé est de trouver \(g: X → Y\), où
  • g est l'une des fonctions de l'ensemble des fonctions possibles G (espace des hypothèses)
• Fonction d'évaluation F indiquent l'espace des fonctions d'évaluation, où
  • \(f: X × Y → R\) telle que g renvoie la fonction d'évaluation la plus élevée.

Formalisation: Apprentissage non supervisé

• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• L'objectif de l'algorithme d'apprentissage non supervisé est
  • trouver la mise en correspondance \(X → Y\)

Formalisation: Apprentissage semi-supervisé

• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• Soit \({(x_1, y_1),...,(x_l, y_l)}\) l'ensemble d'exemples d'exercices étiquetés
• Soit \({x_{l+1},...,x_{l+u}}\) sont les \(u\) ensembles des vecteurs de caractéristiques non étiquetées de \(X\).
• L'objectif de l'algorithme d'apprentissage semi-supervisé est de faire
  • l'apprentissage transductif, c'est-à-dire trouver des étiquettes correctes pour \({x_{l+1},...,x_{l+u}}\).
  • l'apprentissage inductif, c'est-à-dire trouver la bonne mise en correspondance \(X → Y\)

Définition formelle

• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• L'objectif de l'algorithme de classification (ou classificateur) est de trouver \({(x_1, y_1),...,(x_l, y_k)}\), c'est-à-dire l'attribution d'une étiquette connue à chaque vecteur de caractéristique d'entrée, où
  • \(x_i ∈ X \)
  • \(y_i ∈ Y \)
  • \(|X| = l \)
  • \(|Y| = k \)
  • \(l >= k\)

Classificateurs

• Algorithme de classification
• Deux types de classificateurs:
  • Classificateurs binaires attribue un objet à l'une des deux classes
  • Classificateurs multiclasses attribue un objet à une ou plusieurs classes

Classification binaire

Linear Classificateurs

• Fonction linéaire attribuant un score à chaque catégorie possible en combinant le vecteur de caractéristiques d'une instance avec un vecteur de poids, en utilisant un produit de points.
• Formalisation :
  • Soit X être l'espace de saisie des caractéristiques et x_i ∈ X
  • Soit β_k un vecteur de poids pour la catégorie k
  • score(x_i, k) = x_i.β_k, score pour l'attribution de la catégorie k à l'instance x_i. La catégorie qui donne le score le plus élevé est attribuée à la catégorie de l'instance.

Évaluation

Évaluation

Évaluation

Soit

• tp: nombre de vrais postifs
• fp: nombre de faux positifs
• fn: nombre de faux négatifs

Évaluation

Alors

• Précision \[p = \frac{tp}{(tp + fp)}\]
• Rappel (Recall) \[r = \frac{tp}{(tp + fn)}\]

Évaluation

• score F1 est la moyenne harmonique de la précision et du rappel :
• F1-score \[f1 = 2 * \frac{(p * r)}{(p + r)}\]
• F1-score: meilleure valeur à 1 (précision et rappel parfaits) et pire à 0.

Évaluation

• \(F_\beta\)-score utilise un facteur réel positif β, où β est choisi de telle sorte que le rappel est considéré comme β fois plus important que la précision, est :
• \(F_\beta\)-score \[F_\beta = (1 + \beta^2) \cdot \frac{\mathrm{p} \cdot \mathrm{r}}{(\beta^2 \cdot \mathrm{p}) + \mathrm{r}}\]
• Exemple: \(F_2\) score

Évaluation: matrice de confusion

• une matrice qui mesure la qualité d'un système de classification
• chaque ligne de la matrice représente les instances d'une classe prédite
• chaque colonne représente les instances d'une classe réelle
• Toutes les prédictions correctes sont situées dans la diagonale du tableau
• Les erreurs de prédiction seront représentées par des valeurs situées en dehors de la diagonale.

Évaluation: matrice de confusion

Évaluation: matrice de confusion

Classification multiclasse

Classification multiclasse [Aly 2005]

• Transformation en classification binaire
  • L'approche un contre le reste (Un contre tous)
  • L'approche un-contre-un
• Extension de la classification binaire
  • Réseaux de neurones
  • k-voisins les plus proches
• la classification hiérarchique.

Classification multiclasse

Classification multiclasse

One-vs.-rest (One-vs.-all) strategy

Classification multiclasse

One-vs.-rest or One-vs.-all (OvR, OvA) strategy

• Entraîner un seul classificateur par classe, avec les échantillons de cette classe comme échantillons positifs et tous les autres comme négatifs.
• Chaque classificateur produit un score de confiance réel pour sa décision

Classification multiclasse

One-vs.-rest or One-vs.-all (OvR, OvA) strategy

• Entrées :
  • \(L\), un apprenant (algorithme d'entraînement pour les classificateurs binaires)
  • échantillons \(X\)
  • étiquettes \(y\), où \(y_i ∈ \{1,..,K \} \) est l'étiquette de l'échantillon \(X_i\)
• Sortie :
  • une liste de classificateurs \(f_k\), où \(k ∈ \{1,..,K \} \)

Classification multiclasse

One-vs.-rest or One-vs.-all (OvR, OvA) strategy

Prendre des décisions signifie appliquer tous les classificateurs à un échantillon invisible x et prédire l'étiquette k pour laquelle le classificateur correspondant rapporte le score de confiance le plus élevé : \[\hat{y} = \underset{k \in \{1 \ldots K\}}{\arg\!\max}\; f_k(x)\]

Classification multiclasse

One-vs.-one strategy

Classification multiclasse

One-vs.-one strategy

Introduction

Perceptron

• Algorithme pour l'apprentissage supervisé des classificateurs binaires
• Le classificateur binaire est un classificateur qui décide si une entrée donnée appartient ou non à une classe particulière
• Inventé en 1958 par Frank Rosenblatt

Perceptron

1. Source: https://en.wikipedia.org/wiki/File:Perceptron_example.svg

Perceptron

Perceptron: Définition formelle

• Soit \(y = f(z)\) la sortie du perceptron pour un vecteur d'entrée z
• Soit \(N\) le nombre d'exemples d'entraînement
• Soit X l'espace de saisie des caractéristiques
• Soit \({(x_{1}, d_{1}),...,(x_{N}, d_{N})}\) be the N training examples, where
  • \(x_i\) est le vecteur caractéristique de i^ème exemple d'entraînement.
  • \(d_i\) est la valeur de sortie souhaitée
  • \(x_{j,i}\) est la i^ème caractéristique de j^ème exemple d'entraînement.
  • \(x_{j,0} = 1\)

Perceptron: Définition formelle

• Les poids sont représentés de la manière suivante:
  • \(w_i\) est la i^ème valeur du vecteur de poids.
  • \(w_i(t)\) est la i^ème valeur du vecteur de poids à un moment donné t.

Perceptron : Étapes

1. Initialiser les poids et les seuils
2. Pour chaque exemple, \((x_j, d_j)\) dans l'ensemble d'entraînement
   • Calculer la sortie actuelle : \[y_j(t)= f[w(t).x_j]\] \[= f[w_0(t)x_{j,0} + w_1(t)x_{j,1} + w_2(t)x_{j,2} + \dotsb + w_n(t)x_{j,n}]\]
   • Calculer le poids: \[w_i(t + 1) = w_i(t) + r. (d_j-y_j(t))x_{j,i}\]
   \(r\) est le taux d'apprentissage.

Perceptron : Étapes

3. Répétez l'étape 2 jusqu'à l'erreur d'itération \[\frac{1}{s} (Σ |d_j - y_j(t)|)\] est inférieur au seuil spécifié par l'utilisateur \(\gamma\), ou un nombre prédéterminé d'itérations ont été effectuées, où \(s\) est à nouveau la taille de l'ensemble de l'échantillon.

Fonction d'activation: fonction d'identité

Équation

\[f(x)=x\]

Dérivée

\[f'(x)=1\]

Fonction d'activation: pas binaire

Équation

\[f(x) = \begin{cases} 0 & \text{for } x < 0\\ 1 & \text{for } x \ge 0 \end{cases} \]

Dérivée

\[f'(x) = \begin{cases} 0 & \text{for } x \ne 0\\ ? & \text{for } x = 0\end{cases}\]

Fonction d'activation: fonction sigmoïde

Équation

\[f(x)=\sigma(x)=\frac{1}{1+e^{-x}}\]

Dérivée

\[f'(x)=f(x)(1-f(x))\]

Fonction d'activation: TanH

Équation

\[f(x)=\tanh(x)=\frac{(e^{x} - e^{-x})}{(e^{x} + e^{-x})}\]

Dérivée

\[f'(x)=1-f(x)^2\]

Fonction d'activation: Rectified linear unit: ReLU

Équation

\[f(x) = \begin{cases} 0 & \text{for } x \le 0\\ x & \text{for } x > 0\end{cases} = \max\{0,x\}= x \textbf{1}_{x>0}\]

Dérivée

\[f'(x) = \begin{cases} 0 & \text{for } x \le 0\\ 1 & \text{for } x > 0\end{cases}\]

Fonction d'activation: Gaussien

Équation

\[f(x)=e^{-x^2}\]

Dérivée

\[f'(x)=-2xe^{-x^2}\]

Perceptron multiclasse

• Perceptron peut être généralisé à la classification multiclasse.
• Une fonction de représentation d'élément \(f( x , y )\) fait correspondre chaque paire d'entrée/sortie possible à un vecteur d'élément à valeur réelle en dimension finie.
• le vecteur de caractéristique est multiplié par un vecteur de poids \(w\), mais le score obtenu est maintenant utilisé pour choisir parmi de nombreux résultats possibles : \[\hat y = \operatorname{argmax}_y f(x,y) \cdot w.\]
• La réapprentissage se fait par itération sur les exemples, en prédisant un résultat pour chacun, en laissant les poids inchangés lorsque le résultat prédit correspond à l'objectif, et en les modifiant lorsqu'il ne correspond pas. La mise à jour devient : \[w_{t+1} = w_t + f(x, y) - f(x,\hat y)\].

Neurones biologiques

1. https://en.wikipedia.org/wiki/File:Neuron3.png

Réseau de neurones

• collection d'unités ou de nœuds connectés, appelés neurones artificiels, qui modèlent vaguement les neurones d'un cerveau biologique.
• Chaque connexion, comme les synapses dans un cerveau biologique, peut transmettre un signal aux autres neurones.
• Un neurone artificiel qui reçoit un signal le traite ensuite et peut signaler les neurones qui lui sont connectés.
• Le "signal" à une connexion est un nombre réel, et la sortie de chaque neurone est calculée par une fonction non linéaire de la somme de ses entrées.
• Les neurones et les arêtes (connexions) ont généralement un poids qui s'ajuste au fur et à mesure de l'apprentissage.
• Le poids augmente ou diminue la force du signal au niveau d'une connexion.
• Les neurones peuvent avoir un seuil tel qu'un signal n'est envoyé que si le signal global franchit ce seuil.

Réseau de neurones artificiels: les couches

• Les neurones sont agrégés en couches.
• Différentes couches peuvent effectuer des transformations différentes sur leurs entrées.
• Les signaux passent de la première couche (la couche d'entrée) à la dernière couche (la couche de sortie), éventuellement après avoir traversé les couches plusieurs fois.

Réseau de neurones artificiels: l'entraînement

• Les réseaux neuronaux apprennent (ou sont entraînés) en traitant des exemples.
• chaque exemple contient une "entrée" et un "résultat" connus.
• Erreur: L'entraînement d'un réseau de neurones à partir d'un exemple donné est généralement effectué en déterminant la différence entre la sortie traitée du réseau (souvent une prédiction) et une sortie cible
• Le réseau ajuste ensuite ses associations pondérées en fonction d'une règle d'apprentissage et en utilisant cette valeur d'erreur.
• Des ajustements successifs amèneront le réseau de neurones à produire un résultat de plus en plus similaire au résultat cible.

Composants des réseaux de neurones artificiels

• Neurones
• Connexions et poids
• Fonction de propagation

Composants des réseaux de neurones artificiels

Neurones

• Chaque neurone artificiel a des entrées et produit une seule sortie qui peut être envoyée à plusieurs autres neurones.
• Les entrées peuvent être les valeurs caractéristiques d'un échantillon de données externes
• Les sorties des neurones de sortie finale du réseau neuronal accomplissent la tâche
• Fonction d'activation
  • Pour trouver la sortie du neurone, nous prenons d'abord la somme pondérée de tous les intrants
  • Nous ajoutons un terme de biais à cette somme. Cette somme pondérée est parfois appelée l'activation.
  • Cette somme est ensuite passée par une fonction d'activation (généralement non linéaire) pour produire le résultat.

Composants des réseaux de neurones artificiels

Connexions et poids

• Le réseau est constitué de connexions, chaque connexion fournissant la sortie d'un neurone comme entrée à un autre neurone.
• Chaque connexion se voit attribuer un poids qui représente son importance relative
• Un neurone donné peut avoir plusieurs connexions d'entrée et de sortie.

Composants des réseaux de neurones artificiels

Fonction de propagation

• La fonction de propagation calcule l'entrée d'un neurone à partir des sorties de ses prédécesseurs et de leurs connexions comme une somme pondérée.
• Un terme de biais peut être ajouté au résultat de la propagation

Apprentissage profond

• Le mot "profond" dans l'apprentissage profond vient de l'utilisation de multiples couches dans le réseau neuronal.
• Un perceptron linéaire ne peut pas être un classificateur universel. Un perceptron "monocouche" ne peut pas mettre en œuvre le XOR
• Les réseaux d'apprentissage en profondeur permettent un nombre illimité de couches de taille limitée
• Il utilise plusieurs couches pour extraire progressivement des caractéristiques de l'entrée brute.

Composants des réseaux de neurones artificiels

Organisation

• Les neurones sont généralement organisés en plusieurs couches
• Les neurones d'une couche se connectent uniquement aux neurones des couches immédiatement précédente et immédiatement suivante.
• La couche qui reçoit les données externes est la couche d'entrée.
• La couche qui produit le résultat final est la couche de sortie.
• Entre les deux, il y a zéro ou plusieurs couches cachées.

Composants des réseaux de neurones artificiels

Organisation et connectivité

• Les couches peuvent être entièrement connectées, chaque neurone d'une couche étant connecté à chaque neurone de la couche suivante.
• Les couches peuvent être mis en commun (pooling), c'est-à-dire qu'un groupe de neurones dans une couche se connecte à un seul neurone dans la couche suivante, réduisant ainsi le nombre de neurones dans cette couche

Composants des réseaux de neurones artificiels

Organisation et connectivité

• Les réseaux qui permettent des connexions entre les neurones de la même couche ou des couches précédentes sont connus sous le nom de réseaux récurrents.
• les réseaux qui ne permettent pas de cycles entre les couches sont appelés réseaux de neurones en aval (Feedforward neural network)

Réseaux de neurones artificiels: Hyperparamètres

• Un hyperparamètre est un paramètre constant dont la valeur est fixée avant le début du processus d'apprentissage.
• Les valeurs des paramètres sont obtenues par apprentissage.
• Exemples
  • le taux d'apprentissage
  • le nombre de couches cachées
  • la taille des échantillons.
  • ...

Exemple: Tensorflow

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD

# Créer un modèle séquentiel
model = Sequential()
model.add(Dense(4, activation='relu', input_shape=(3,)))
model.add(Dense(units=2, activation='softmax'))

# Compilation du modèle
sgd = SGD(lr=0.01)
model.compile(loss='mean_squared_error',
   optimizer=sgd,metrics=['accuracy'])

Réseau de neurones en aval (Feedforward neural networks)

• Les connexions entre les nœuds ne forment pas un cycle
• Les informations se déplacent des nœuds d'entrée vers les nœuds de sortie, en passant par les nœuds cachés (le cas échéant).
• L'information ne circule que dans un seul sens, vers l'avant

Perceptron simple couche

Perceptron multicouche

Rétropropagation du gradient (Backpropagation)

• La rétropropagation est une méthode permettant d'ajuster les poids de connexion pour compenser chaque erreur constatée lors de l'apprentissage
• Le montant de l'erreur est effectivement réparti entre les connexions.
• calcule le gradient de la fonction de perte par rapport aux poids du réseau pour un seul exemple d'entrée-sortie.
• fonctionne en calculant le gradient de la fonction de perte par rapport à chaque poids selon la règle de la chaîne

Réseau de neurones récurrents

• Un réseau de neurones où les connexions entre les nœuds forment un graphe dirigé le long d'une séquence temporelle, lui permettant de présenter un comportement dynamique temporel.
• Ils peuvent utiliser leur état interne (mémoire) pour traiter des séquences d'entrées de longueur variable
• Applications
  • la reconnaissance de l'écriture manuscrite
  • la reconnaissance vocale

Réseau de neurones récurrents

Réseau récurrent à mémoire court et long terme

Long short-term memory (LSTM) network

Réseau récurrent à mémoire court et long terme

Long short-term memory (LSTM) network

• LSTM a des connexions de retour d'information
• Une unité LSTM commune est composée d'une cellule, d'une porte d'entrée, d'une porte de sortie et d'une porte d'oubli.
• La cellule se souvient de valeurs sur des intervalles de temps arbitraires et les trois portes régulent le flux d'informations entrant et sortant de la cellule.

Réseau récurrent à mémoire court et long terme

Long short-term memory (LSTM) network

• LSTM a des connexions de retour d'information

Réseaux de neurones convolutionnels

Réseaux de neurones convolutionnels

• Analyse des images
• Utilise la convolution, une opération mathématique linéaire
• Une couche d'entrée et une couche de sortie
• Plusieurs couches cachées, constituées de couches convolutives

Réseaux de neurones convolutionnels

• Ils considèrent le modèle hiérarchique des données et assemblent des modèles plus complexes en utilisant des modèles plus petits et plus simples.
• Un réseau neuronal convolutif est constitué d'une couche d'entrée et d'une couche de sortie, ainsi que de plusieurs couches cachées.
• Les couches cachées d'un CNN consistent généralement en une série de couches convolutionnelles qui se convoluent avec une multiplication
• La fonction d'activation est généralement une couche RELU, et est ensuite suivie par des convolutions supplémentaires telles que des couches de regroupement, des couches entièrement connectées et des couches de normalisation

Noyau (traitement d'image)

Identité

\( \begin{matrix} \ \ 0 &\ \ 0 &\ \ 0 \\ \ \ 0 &\ \ 1 &\ \ 0 \\ \ \ 0 &\ \ 0 &\ \ 0 \end{matrix} \)

La détection de contours

\( \begin{matrix} \ \ 1 & 0 & -1 \\ \ \ 0 & 0 & \ \ 0 \\ -1 & 0 & \ \ 1 \end{matrix} \)

Noyau (traitement d'image)

Box blur

\( \frac{1}{9} \begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{matrix} \)

Flou de Gauss 3 × 3

\( \frac{1}{16} \begin{matrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{matrix} \)

Convolution matricielle

\[ \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1n} \\ x_{21} & x_{22} & \cdots & x_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ x_{m1} & x_{m2} & \cdots & x_{mn} \\ \end{bmatrix} * \begin{bmatrix} y_{11} & y_{12} & \cdots & y_{1n} \\ y_{21} & y_{22} & \cdots & y_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ y_{m1} & y_{m2} & \cdots & y_{mn} \\ \end{bmatrix} = \sum^{m-1}_{i=0} \sum^{n-1}_{j=0} x_{(m-i)(n-j)} y_{(1+i)(1+j)} \]

Max pooling

Exemple: Tensorflow (réseaux de neurones convolutionnels)

            
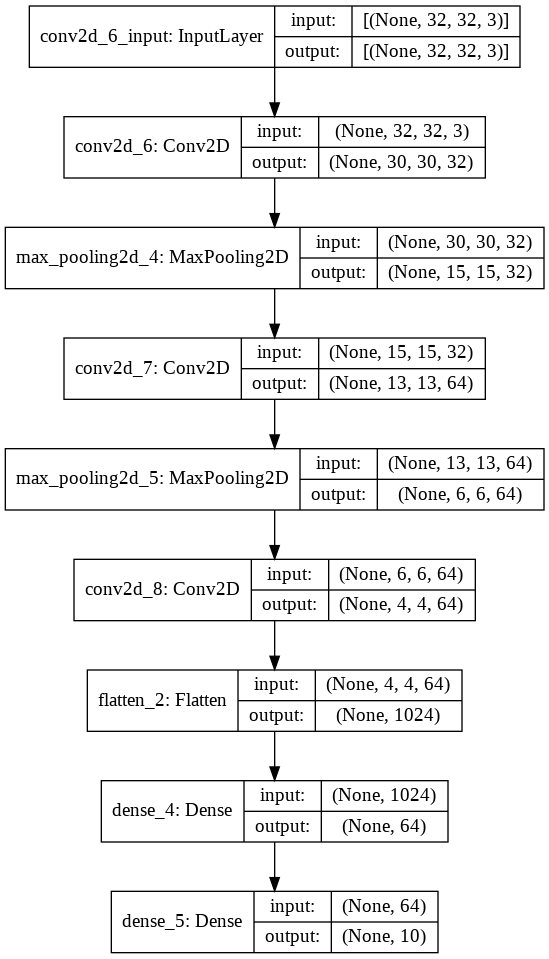
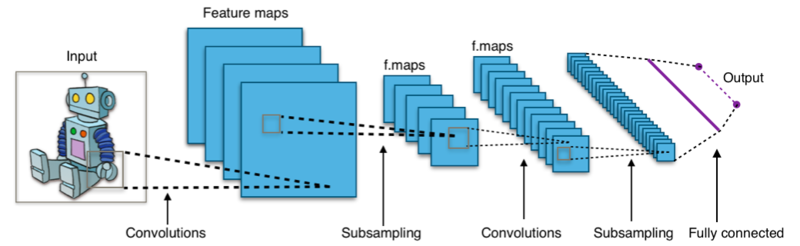
import tensorflow as tf

from tensorflow.keras import datasets, layers, models

(train_images, train_labels), (test_images, test_labels) = datasets.cifar10.load_data()
train_images, test_images = train_images / 255.0, test_images / 255.0

# Créer un modèle séquentiel (réseaux de neurones convolutionnels)
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)))
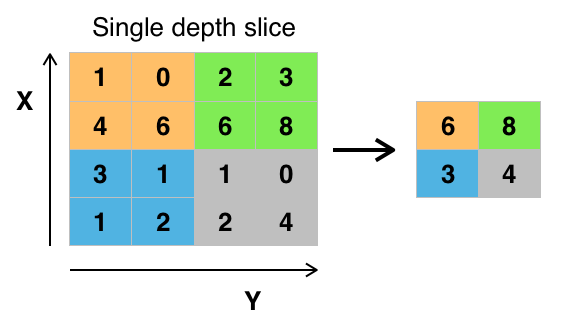
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
            
          

Exemple: Tensorflow (réseaux de neurones convolutionnels)

            
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10)

#Compilation du modèle
model.compile(optimizer='adam',
   loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
   metrics=['accuracy'])

history = model.fit(train_images, train_labels, epochs=10,
   validation_data=(test_images, test_labels))
            
          

Exemple: Tensorflow (réseaux de neurones convolutionnels)

Articles de recherche

• [Aly 2005] Aly, Mohamed. Survey on Multiclass Classification Methods. 2005.
• [Jaakkola 2019] Jaakkola, H., et al. “Artificial Intelligence Yesterday, Today and Tomorrow.” 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), 2019, pp. 860–67. IEEE Xplore
• [Pan 2016] Pan, Yunhe, “Heading toward Artificial Intelligence 2.0.” Engineering, vol. 2, no. 4, Dec. 2016, pp. 409–13. www.sciencedirect.com,

Web

• https://en.wikipedia.org/wiki/Perceptron
• https://en.wikipedia.org/wiki/Multiclass_classification
• http://scikit-learn.org/stable/
• https://en.wikipedia.org/wiki/Multilayer_perceptron
• https://en.wikipedia.org/wiki/Feedforward_neural_network
• https://en.wikipedia.org/wiki/Recurrent_neural_network
• https://en.wikipedia.org/wiki/Long_short-term_memory
• https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Perceptron.html
• https://en.wikipedia.org/wiki/Activation_function

Couleurs

• Color Tool - Material Design

Images

• Wikimedia Commons