Apprentissage machine
John Samuel
CPE Lyon
Year: 2020-2021
Email: john(dot)samuel(at)cpe(dot)fr


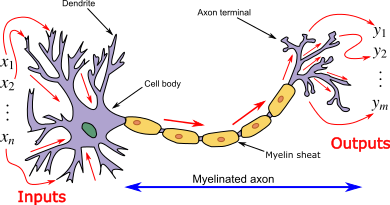
Soit
Alors


Prendre des décisions signifie appliquer tous les classificateurs à un échantillon invisible x et prédire l'étiquette k pour laquelle le classificateur correspondant rapporte le score de confiance le plus élevé : \[\hat{y} = \underset{k \in \{1 \ldots K\}}{\arg\!\max}\; f_k(x)\]


\[f(x)=x\]
\[f'(x)=1\]
\[f(x) = \begin{cases} 0 & \text{for } x < 0\\ 1 & \text{for } x \ge 0 \end{cases} \]
\[f'(x) = \begin{cases} 0 & \text{for } x \ne 0\\ ? & \text{for } x = 0\end{cases}\]
\[f(x)=\sigma(x)=\frac{1}{1+e^{-x}}\]
\[f'(x)=f(x)(1-f(x))\]
\[f(x)=\tanh(x)=\frac{(e^{x} - e^{-x})}{(e^{x} + e^{-x})}\]
\[f'(x)=1-f(x)^2\]
\[f(x) = \begin{cases} 0 & \text{for } x \le 0\\ x & \text{for } x > 0\end{cases} = \max\{0,x\}= x \textbf{1}_{x>0}\]
\[f'(x) = \begin{cases} 0 & \text{for } x \le 0\\ 1 & \text{for } x > 0\end{cases}\]
\[f(x)=e^{-x^2}\]
\[f'(x)=-2xe^{-x^2}\]