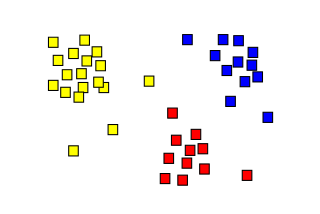
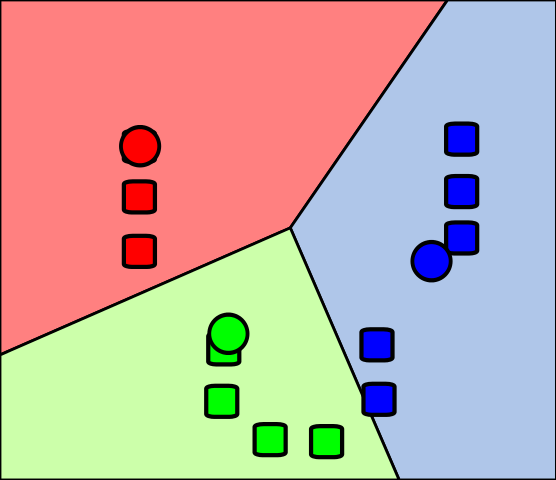
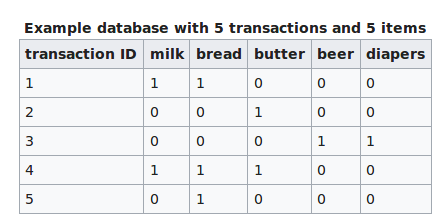
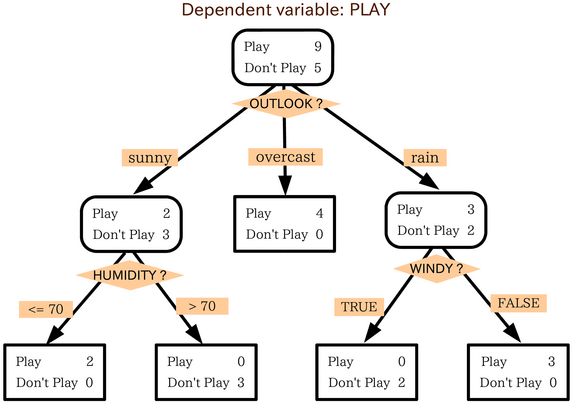
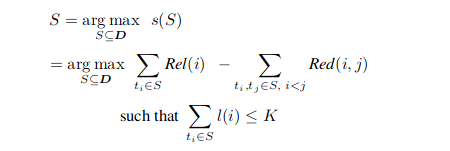Data Mining
John Samuel
CPE Lyon
Year: 2019-2020
Email: john(dot)samuel(at)cpe(dot)fr











.jpg)



.png)
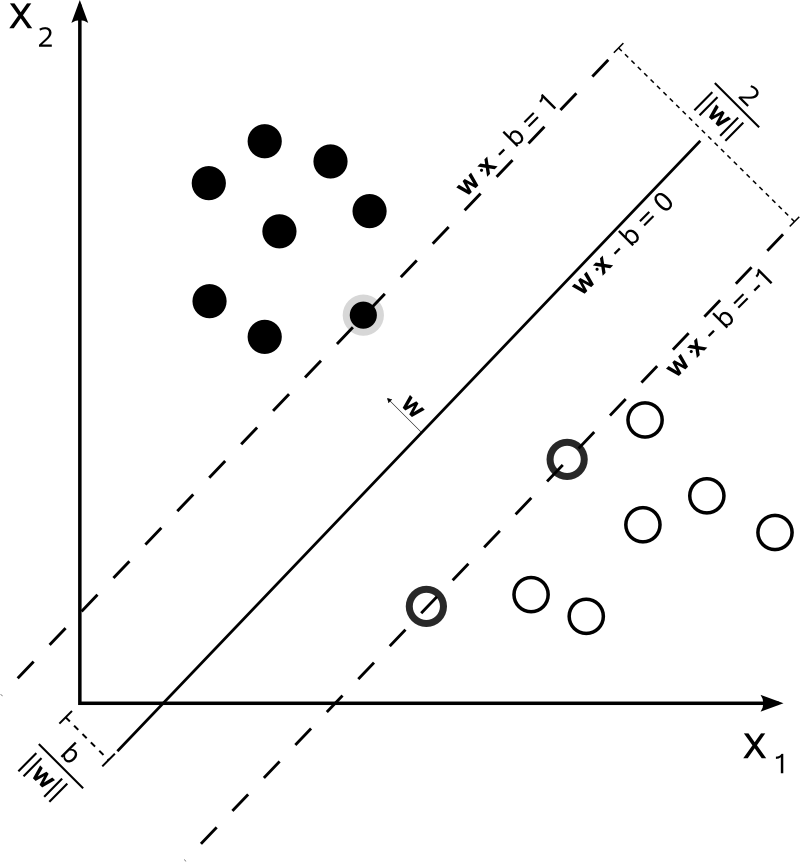
Let
Then